Equation Of Ellipse And Hyperbola
This work is licensed under a creative commons license.
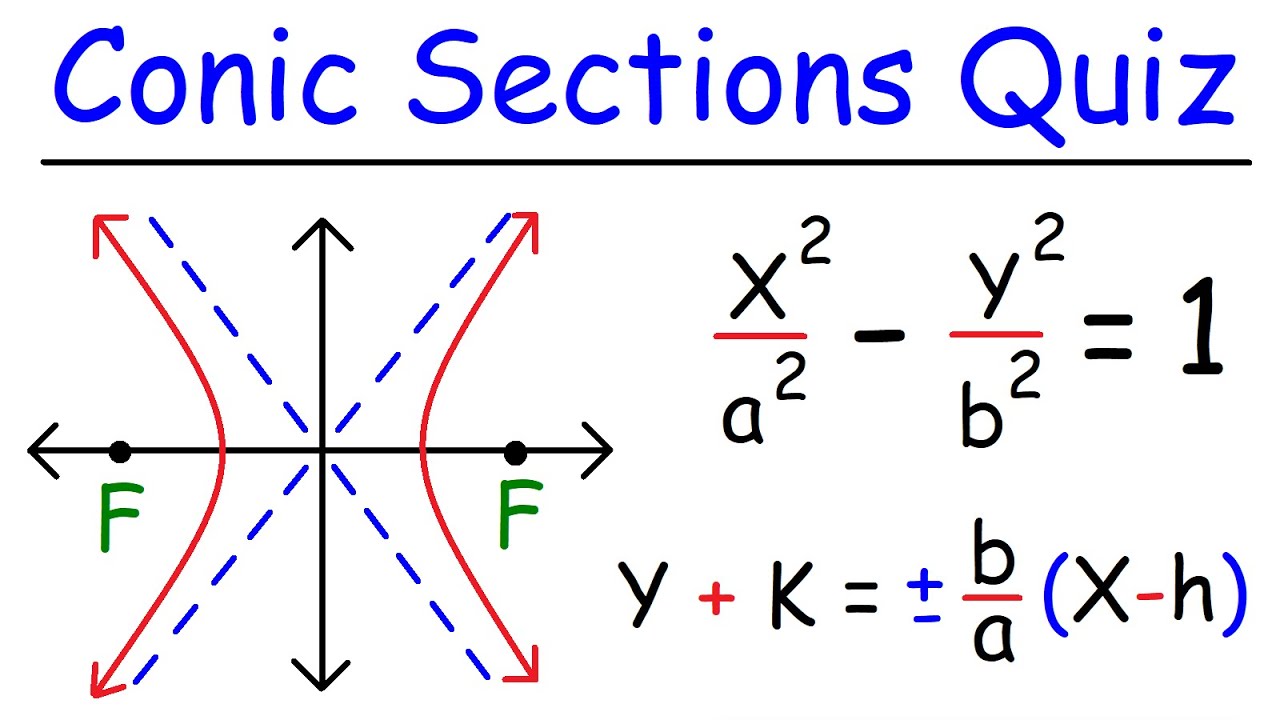
Equation of ellipse and hyperbola. In mathematics a hyperbola plural hyperbolas or hyperbolae is a type of smooth curve lying in a plane defined by its geometric properties or by equations for. Problems with detailed solutions on equation of hyperbola. Equation of hyperbola graphing problems. Problems with detailed solutions on the hyperbola equation.
If cartesian coordinates are introduced such that the origin is the center of the ellipse and the x axis is the major axis and the foci are the points. Learn about the four conic sections and their equations. Circle ellipse parabola and hyperbola. An ellipse is a curve that is the locus of all points in the plane the sum of whose distances r1 and r2 from two fixed points f1 and f2 the foci separated by a.
A hyperbola plural hyperbolas. 45 is a conic section defined as the locus of all points p in the plane the difference of whose distances r1f1p. Think of a hyperbola as a mix of two parabolas each one a perfect mirror image of the other each opening away from one another. The vertices of these parabolas.
Lake tahoe community college math department home page. E mail questions and suggestions.
What Is The Difference Between Identifying A Parabola Ellipse
Links Forward Conic Sections
How Do You Determine Circle Parabola Ellipse Or Hyperbola From
Conic Sections Circle Parabola Ellipse And Hyperbola Algebra
Conic Sections Circles Ellipses Parabolas Hyperbola How To
Conic Sections
Warm Up Find The Equation In Standard Form Of Then Give The
Conic Sections Aerospace Engineering
Why Is The Differential Equation Of Ellipse And Hyperbola The Same
Parametric Equations Of Ellipses And Hyperbolas
Equations Of Hyperbolas Math Stuff Math Love Math Calculus
Conic Sections
Conic Sections Circle Ellipse Hyperbola Parabola Wall Posters
Conic Sections And Standard Forms Of Equations
Fp3 Conics Ellipses And Hyperbolas A Minimum Of Blind Calculation
Conic Sections Circle Ellipse Hyperbola Parabola Wall Posters
Conic Sections Eccentricity Ppt Video Online Download
The Twilight Saga Ellipse A Guide To Conics I M An Awkward Turtle
Equations For Hyperbola Ellipse Parabola Circle Tessshebaylo
Ellipses Aims Tutorial 10 2
Parametric Equations Of Ellipses And Hyperbolas
Solution Find The Equation Of The Hyperbola With Vertices 4 2
Eccentricity Of Conic Sections Study Com
Polar Equations Of Conics
Conic Sections Parabolas Hyperbolas Ellipses Circles Graphing
Equations Of Ellipses And Hyperbolas Ppt Video Online Download
Mathwords Hyperbola
Equations Of Ellipses And Hyperbolas Ppt Video Online Download
Systems Of Equations Solved Graphically
Conic Sections
Solved Classify The Graph Of The Equation As A Circle A
Equation Of Hyperbola Standard Equations Derivatives Observations
Conic Sections Circle Ellipse Hyperbola Parabola Wall Posters
Equations Of Ellipses And Hyperbolas Ppt Video Online Download
Conic Sections Hyperbola Find Equation Given Foci And Vertices
Conic Section Wikipedia
Hyperbolas
Day 7 Hw Test D Part 2 Circle Parabola Ellipse Hyperbola Youtube
Polar Equations Of Conics
Circles Parabolas Ellipses And Hyperbolas Ppt Download
Definition And Examples Directrix Define Directrix Pre Calculus
Conic Sections Precalculus Math Khan Academy
Sparknotes Sat Subject Test Math Level 2 Other Important Graphs
Ppt W Riting And G Raphing E Quations Of C Onics Powerpoint
Conic Sections And Standard Forms Of Equations
Hyperbolas The Equation Of A Hyperbola Is Almost Exactly That Of An
Solution What Is The Equation Of The Asymptote Of The Hyperbola X 2
Conic Section Wikipedia
A The Dispersion Surfaces Composed Of The Ellipse And Hyperbola In
Hyperbola Conic Section Equation Graph Of A Function Ellipse
